Funkce

07 Mar 2023

• Funkce a její graf
  • Definice funkce
  • Graf funkce
  • Obor hodnot funkce
  • Rostoucí a klesající funkce
  • Sudá a lichá funkce
  • Omezená funkce
  • Minimum a maximum funkce
  • Inverzní funkce
  • Lineární funkce
    • Definice lineární funkce
    • Graf lineární funkce
    • Některé vlastnosti lineárních funkcí
  • Kvadratické funkce
    • Grafy kvadratických funkcí
    • Grafy kvadratických funkcí při řešení rovnic a nerovnic
  • Lineární lomené funkce
    • Nepřímá úměrnost
  • Mocninné funkce
    • Mocninné funkce s přirozeným exponentem
    • Mocninné funkce s celým exponentem
    • Definice $n$-té mocniny
    • Počítání s odmocninami
    • Mocniny s racionálním exponentem
  • Exponenciální funkce
    • Exponenciální rovnice
  • Logaritmické funkce
    • Logaritmus
    • Věty o logaritmech
  • Goniometrické funkce
    • Periodická funkce
    • Goniometrické funkce ostrého úhlu
    • Velikost úhlu v obloukové míře
    • Funkce sinus a kosinus
    • Funkce tangens a kotangens

---

Funkce a její graf

Definice funkce

Funkce na množině $A \subset \R$ je předpis, který každému číslu z množiny $A$ přiřazuje právě jedno reálné číslo. Množina $A$ se nazývá definiční obor funkce.

Číslo $f(x_0)$ budeme nazývat hodnota funkce $f$ v bodě $x_0$ nebo funkční hodnota.

Dále platí, že v bodě $x_0$ může funkce nabývat pouze jedné funkční hodnoty.

Funkci můžeme mít zadanou:

• předpisem
• tabulkou bodů a funkčních hodnot

Graf funkce

Graf funkce $f$ ve zvolené soustavě souřadnic $Oxy$ v rovině je množina všech bodů $X[x, f(x)]$, kde $x$ patří do definičního oboru funkce $f$.

Obor hodnot funkce

Obor hodnot funkce $f$ je množina všech $y \in \R$, ke kterým existuje aspoň jedno $x$ z definičního oboru funkce $f$ tak, že $y = f(x)$.

Rostoucí a klesající funkce

Funkce $f$ se nazývá rostoucí, právě když pro všechna $x_1, x_2 \in D_f$ platí: Je-li $x_1 < x_2$, pak $f(x_1) < f(x_2)$.
Funkce $f$ se nazývá klesající, právě když pro všechna $x_1, x_2 \in D_f$ platí: Je-li $x_1 < x_2$, pak $f(x_1) > f(x_2)$.

Funkce $f$ nemusí být na celém definičním oboru jen rostoucí nebo jen klesající. V jedné části jejího definičního oboru hodnoty funkce s růstem hodnot proměnné $x$ rostou, ve druhé části klesají.

Abychom mohli přesněji popsat průběh funkce, vyslovíme ještě jednu definici:

Je dána funkce $f$, $J$ je interval, který je částí jejího definičního oboru $(J \subset D_f)$.
Funkce $f$ se nazývá rostoucí v intervalu $J$, právě když pro všechna $x_1, x_2 \in J$ platí: je-li $x_1 < x_2$, pak $f(x_1) < f(x_2)$.
Funkce $f$ se nazývá klesající v intervalu $J$, právě když pro všechna $x_1, x_2 \in J$ platí: je-li $x_1 < x_2$, pak $f(x_1) < f(x_2)$.

Uvedeme další důležitou vlastnost, kterou mohou funkce mít:

Funkce $f$ se nazývá prostá, právě když pro všechna $x_1, x_2 \in D_f$ platí: Je-li $x_1 \ne x_2$, pak $f(x_1) \ne f(x_2)$.

Je-li funkce rostoucí, pak je prostá.
Je-li funkce klesající, pak je prostá.

Sudá a lichá funkce

Funkce $f$ se nazývá sudá, právě když zároveň platí:

1. Pro každé $x \in D_f$ je také $-x \in D_f$.
2. Pro každé $x \in D_f$ je $f(-x) = f(x)$.

Graf sudé funkce je souměrný podle osy $y$. Příkladem sudé funkce je např. $y = -\lvert x\rvert$.

Funkce $f$ se nazývá lichá, právě když zároveň platí:

1. Pro každé $x \in D_f$ je také $-x \in D_f$.
2. Pro každé $x \in D_f$ je $f(-x) = -f(x)$.

Graf liché funkce je souměrný podle počátku soustavy souřadnic $Oxy$. Příkladem liché funkce je např. $y= 2x$.

Omezená funkce

Funkce $f$ se nazývá zdola omezená, právě když existuje číslo $d$ takové, že pro všechna $x \in D_f$ je $f(x) \geq d$.
Funkce $f$ se nazývá shora omezená, právě když existuje číslo $h$ takové, že pro všechna $x \in D_f$ je $f(x) \leq h$.
Funkce $f$ se nazývá omezená, právě když je zdola omezená a zároveň shora omezená.

Minimum a maximum funkce

Říkáme, že funkce $f$ má v bodě $a$ maximum, právě když pro všechna $x \in D_f$ je $f(x) \leq f(a)$.
Říkáme, že funkce $f$ má v bodě $b$ minimum, právě když pro všechna $x \in D_f$ je $f(x) \geq f(b)$.

Inverzní funkce

Inverzní funkce k prosté funkci $f$ je funkce $f^{-1}$, pro kterou platí:

1. $D_{f^{-1}} = H$,
2. Každému $y \in D_{f^{-1}}$ je přiřazeno právě to $x \in D_f$, pro které je $f(x)=y$

Grafy funkcí $f$ a $f^{-1}$ sestrojené v téže soustavě $Oxy$ se stejnou délkovou jednotkou na obou osách jsou souměrně sdruženy podle přímky $y=x$.

Lineární funkce

Definice lineární funkce

Lineární funkce je každá funkce na množině $\R$, která je dána ve tvaru

$$y = ax + b,$$

kde $a, b$ jsou reálná čísla.
Speciálním případem lineárních funkcí jsou funkce, pro něž je $a=0$, tj. funkce

$$y=b,$$

které nazýváme konstantní funkce.
Pro lineární funkce, vyjádřené ve tvaru

$$y=ax,$$

tj. pro funkce dané vzorcem $y=ax+b$, v němž je $b=0$, užíváme také název přímá úměrnost.

Graf lineární funkce

Grafem lineární funkce je přímka.

Některé vlastnosti lineárních funkcí

Lineární funkce $y=ax+b$

• je rostoucí pro $a>0$,
• je klesající pro $a<0$,
• není prostá, je-li $a=0$.

Pro číslo $a$ v lineární funkci $f: y= ax+b$ platí

$$a = \frac{f(x_2)-f(x_1)}{x_2-x_1},$$

kde $x_1, x_2$ jsou libovolně zvolená, vzájemně různá reálná čísla.

sem bych chtěla vložit obrázek

Kvadratické funkce

Kvadratická funkce je každá funkce na množině $\R$ daná ve tvaru

$$y=ax^2+bx+c,$$

kde $a \in \R \setminus \{ 0 \}, b,c \in \R$.

Grafy kvadratických funkcí

Grafem funkce $y=x^2$ je plynulá nepřerušovaná křivka, která se nazývá parabola.

obrazek

Z obrázku lze usoudit, že funkce $y=x^2$ má tyto vlastnosti:

• jejím oborem hodnot je interval $<0, \infty)$;
• funkce je v intervalu $(- \infty, 0>$ klesající,
• v intervalu $<0, + \infty)$ rostoucí
• v bodě $0$ má minimum
• v žádném bodě maximum
• je zdola omezená
• není shora omezená
• je sudá

Grafy kvadratických funkcí při řešení rovnic a nerovnic

Pomocí grafů kvadratických funkcí lze řešit kvadratické rovnice i nerovnice (předem je všem nutné převést tyto rovnice a nerovnice na anulovaný tvar). Zjistíme, ve kterých bodech je hodnota funkce $f$ rovna nule.

Lineární lomené funkce

Lineární lomená funkce je každá funkce na množině $\R \setminus \{ - \frac{d}{c} \}$ vyjádřená ve tvaru

$$y= \frac{ax+b}{cx+d},$$

kde $a,b,c,d$ jsou reálná čísla, $c \ne 0$ a $ad-bc \ne 0$.

Grafem každé lineární lomené funkce je hyperbola, kterou získáme z grafu funkce $y= \frac{k}{x}$ pomocí posunutí.

Nepřímá úměrnost

Nepřímá úměrnost je každá funkce na množině $\R \setminus \{ 0 \}$ daná ve tvaru

$$y= \frac{k}{x},$$

kde $k$ je reálné číslo různé od nuly.

Graf funkce $y= \frac{k}{x}$ je křivka, která se nazývá rovnoosá hyperbola.

Mocninné funkce

Mocninné funkce s přirozeným exponentem

Pro všechna $a \in \R$ a pro všechna $n \in \N$ definujeme

$$a^n = a \cdot a \cdot \ldots \cdot a \rightarrow n-krát$$

$a \ldots$ základ mocniny (mocněnec)
$x \ldots$ exponent (mocnitel)

$$y= x^n ; n \in \N$$

$n$ liché
obrázek Vlastnosti:

• Oborem hodnot je $\R$
• Je rostoucí
• Je lichá
• Není shora omezená, ani zdola omezená
• Nemá maximum, ani minimum

$n$ sudé
obrázek Vlastnosti:

• Oborem hodnot $<0,+ \infty )$
• Je rostoucí v $<0, + \infty )$
• Je klesající v $(- \infty , 0>$
• Je sudá
• Je zdola omezená, není shora omezená
• V bodě $0$ má minimum, v žádném bodě nemá maximum

Mocninné funkce s celým exponentem

Funkce

$$y= x_n ; n \in \Z^{-}$$

$-n$ liché obrazek Vlastnosti:

• Oborem hodnot je $\R \setminus \{ 0 \}$
• Je klesající v $(- \infty , 0), (0, + \infty )$
• Není ani zdola omezená, ani shora omezená
• Nemá žádné maximum, ani minimum
• Je lichá

$-n$ sudé obraze Vlastnosti:

• Oborem hodnot je $\R^+$
• Je rostoucí v $(- \infty , 0)$
• Je klesající v $(0, + \infty)$
• Je zdola omezená, není shora omezená
• Nemá v žádném bodě ani maximum, ani minimum
• Je sudá

Definice $n$-té mocniny

Pro každé $n \in \N$ je $n$-tá odmocnina z nezáporného čísla $a$ takové nezáporné číslo $b$, pro než platí $b^n = a$. Budeme zapisovat

$$b= \sqrt[n]{a}$$

Číslo $n$ se nazývá odmocnitel (exponent odmocniny), číslo $a$ odmocněnec (základ mocniny).

Počítání s odmocninami

Pro všechna nezáporná reálná čísla $a,b$ a pro každé přirozené číslo $n$ platí:

$$\sqrt[n]{a} \cdot \sqrt[n]{b} = \sqrt[n]{ab}$$

“Součin $n$-tých odmocnin čísel $a,b$ je roven $n$-té odmocnině jejich součinu.”

Pro každé nezáporné reálné číslo $a$, každé kladné reálné číslo $b$ a každé přirozené číslo $n$ platí:

$$\frac{\sqrt[n]{a}}{\sqrt[n]{b}} = \sqrt[n]{\frac{a}{b}}$$

“Podíl $n$-tých odmocnin čísel $a,b$ je roven $n$-té odmocnině jejich podílu.”

Pro každé celé číslo $s$, každé kladné reálné číslo $a$ a každé přirozené číslo $n$ platí:

$$( \sqrt[n]{a} )^s = \sqrt[n]{a^s}$$

Pro všechna přirozená čísla $m,n$ a pro každé nezáporné reálné číslo $a$ platí:

$$\sqrt[m]{\sqrt[n]{a}} = \sqrt[mn]{a}$$

Mocniny s racionálním exponentem

Pro každé kladné reálné číslo $a$, pro každé celé číslo $m$ a pro každé přirozené číslo $n$ je

$$a^{\frac{m}{n}} = \sqrt[n]{m}$$

Číslo $a$ budeme nazývat základ mocniny čili mocněnec, číslo $\frac{m}{n}$ se nazývá exponent čili mocnitel.

Pro všechna kladná reálná čísla $a,b$ a pro všechna racionální čísla $r,s$ je

$$\begin{align} a^r \cdot a^s &= a^{r+s}\notag\\ (a^r)^s &= a^{rs}\notag\\ \frac{a^r}{a^s} &= a^{r-s}\notag\\ (ab)^r &= a^r \cdot b^r\notag\\ \end{align}$$

Exponenciální funkce

Exponenciální funkce o základu $a$ je funkce na množině $\R$ vyjádřená ve tvaru

$$y=a^x,$$

kde $a$ je kladné číslo různé od $1$.

Pro $a>1$ je funkce rostoucí, a tedy prostá a pro $0<a<1$ je funkce klesající, a tedy prostá.

Další vlastnosti:

• Definiční obor je $\R$
• Obor hodnot je $(0;+ \infty )$
• Je zdola omezená, není shora omezená
• Nemá ani maximum ani minimum
• Funkční hodnota v bodě $0$ je rovna $1$

Exponenciální rovnice

$a \ldots$ základ mocniny (mocněnec)
$x \ldots$ exponent (mocnitel)

Pro všechna reálná čísla $x_1, x_2$ platí: je-li $x_1 \ne x_2$, pak $a^{x_1} \ne a^{x_2}$, čili

$$a^{x_1} = a^{x_2}, x_1 = x_2.$$

Věty užívané při řešení exponenciálních rovnic:

Logaritmické funkce

Logaritmická funkce o základu $a$ je funkce, která je inverzní k exponenciální funkci $y=a^x$ ; $a$ je libovolné kladné číslo různé od jedné.

Čteme “logaritmus $x$ o základu $a$”. V souladu s tímto označením budeme logaritmickou funkci $f^{-1}$ o základu $a$ zapisovat ve tvaru

$$y= \log_ax.$$

Definičním oborem logaritmické funkce je množina $(0, + \infty)$.

$$y= \log_ax ; a\in \R \setminus \{ 1 \}$$

Pro $a>1$ je funkce rostoucí, a tedy prostá a pro $0<a<1$ je funkce klesající, a tedy prostá.

Další vlastnosti:

• Obor hodnot je $\R$
• Není ani shora, ani zdola omezená
• Nemá ani minimum, ani maximum
• Funkční hodnota v bodě $1$ je rovna $0$

Logaritmus

Uvažujme logaritmickou funkci $y= \log_ax$, kde základ $a$ je libovolné kladné číslo různé od jedné. Určit její funkční hodnotu v bodě $r^2$, tj. logaritmus čísla $r$ o základu $a$ znamená najít takové číslo, kterým musíme umocnit základ $a$, abychom obdrželi číslo $r$:

$$r=a^{log_ar}.$$

Věty o logaritmech

Pro každé $a>0, a \ne 1$ a pro všechna kladná reálná čísla $r,s$ je

$$\log_a(r \cdot s) = \log_ar + \log_as.$$

“Logaritmus součinu dvou kladných čísel je roven součtu logaritmů jednotlivých činitelů.”

Pro každé $a>0, a \ne 1$ a pro všechna kladná reálná čísla $r, s$ je

$$\log_a \frac{r}{s} = \log_ar - \log_as.$$

“Logaritmus podílu dvou kladných čísel je roven rozdílu logaritmů dělence a dělitele (v tomto pořadí).”

Pro každé $a>0, a \ne 1$, pro všechna $r \in \R^+$ a pro všechna $s \in \R$ je

$$\log_ar^s = s \cdot \log_ar.$$

“Logaritmus mocniny kladného čísla je roven součinu mocnitele a logaritmu základu mocniny.”

Logaritmy o základu $10$ obvykle označujeme jako dekadické logaritmy a zapisujeme je pouze $\log x$ a čteme “logaritmus x.”

Goniometrické funkce

Periodická funkce

Funkce $f$ se nazývá periodická funkce, právě když existuje takové číslo $p > 0$, že pro každé $k \in \Z$ platí následující podmínky:

• Je-li $x \in D_f$, pak $x + kp \in D_f$;
• $f(x +kp) = f(x)$.
  Číslo $p$ se nazývá perioda funkce $f$.

Goniometrické funkce ostrého úhlu

Sinus $\alpha$ je poměr délky odvěsny protilehlé k úhlu $\alpha$ a délky přepony pravoúhlého trojúhelníku.

$$\sin \alpha = \frac{a}{c}$$

Kosinus $\alpha$ je poměr délky odvěsny přilehlé k úhlu $\alpha$ a délky přepony.

$$\cos \alpha = \frac {b}{c}$$

Tangens $\alpha$ je poměr délek odvěsny protilehlé k úhlu $\alpha$ a odvěsny přilehlé.

$$\tan \alpha = \frac{a}{b}$$

Kotangens $\alpha$ je poměr délek odvěsny přilehlé k úhlu $\alpha$ a odvěsny protilehlé.

$$\cot \alpha = \frac{b}{a}$$

Velikost úhlu v obloukové míře

Radián je středový úhel, který přísluší na jednotkové kružnici oblouku o délce $1$

Funkce sinus a kosinus

obrazek

Funkcí sinus se nazývá funkce na množině $\R$, kterou je každému číslu $x \in \R$ přiřazeno číslo $y_L$.
Funkcí kosinus se nazývá funkce na množině $\R$, kterou je každému číslu $x \in \R$ přiřazeno číslo $x_L$.

Obě funkce jsou periodické, jejich nejmenší perioda je $2 \pi$.

Pro každé $k \in \Z$ a pro každé $x \in \R$

$$\sin(x + k \cdot 2 \pi) = \sin x,$$ $$\cos(x + k \cdot 2 \pi) = \cos x.$$

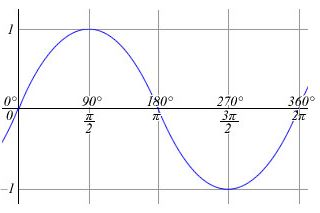
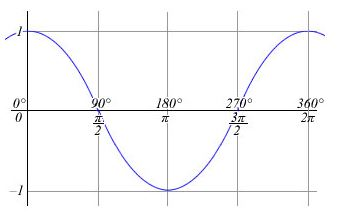
Vlastnosti funkcí sinus a kosinus:

• Obě funkce jsou shora i zdola omezené
• Funkce $y = \sin x, x \in <0, 2 \pi)$ má v bodě $x_1 = \frac{\pi}{2}$ maximum, v bodě $x_2 = \frac{3}{2} \pi$ minimum
• Funkce $y = \cos x, x \in <0, 2 \pi)$ má v bodě $x_3 = 0$ maximum, v bodě $x_4 = \pi$ minimum.
• Oborem hodnot obou funkcí je interval $<-1,1>$
• Funkce sinus je lichá a funkce kosinus je sudá.

Pro každé $x \in \R$

$$\sin(-x) = - \sin x,$$ $$\cos(-x) = \cos x.$$

Sinusoida

• Grafem funkce sinus je tzv. sinusoida

Kosinusioda

• Grafem funkce kosinus je tzv. kosinusoida

Funkce tangens a kotangens

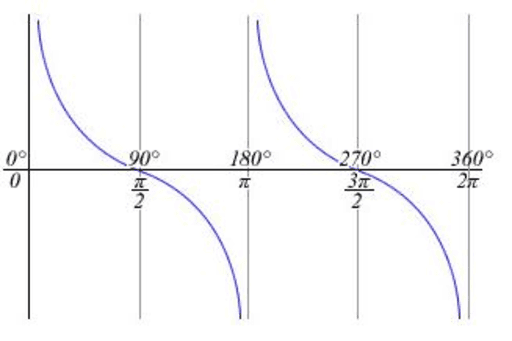
Funkcí tangens se nazývá funkce daná vztahem

$$y = \frac{\sin x}{\cos x}.$$

Funkcí kotangens se nazývá funkce daná vztahem

$$y = \frac{\cos x}{\sin x}.$$

Tyto funkce zapisujeme

$$y = \tg x,$$ $$y = \cotg x.$$

Vlastnosti funkcí tangens a kotangens:

• Definičním oborem funkce $y = \tg x$ je množina všech $x \in \R$, pro něž $x \neq (2k +1) \frac{\pi}{2}$, kde $k \in \Z$
• Definičním oborem funkce $y= \cotg x$ je množina všech $x \in \R$, pro něž $x \neq k \pi$
• Funkce tangens a kotangens jsou liché funkce.
• Obě funkce jsou periodické a jejich nejmenší perioda je $\pi$

Graf funkce tangens

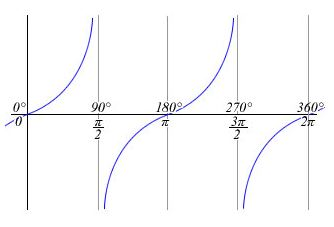
Graf funkce kotangens

---