Chaos

18 Dec 2022

Záznam přednášky ze Smrště 2022.

• Historie chaosu
  • Deterministické systémy - Newtonovské zákony
• Definice chaosu
  • Dynamické soustavy
  • Chaotické chování
  • Motýlí efekt
  • Atraktory
    • Lorenzův atraktor
    • Rösslerův atraktor
    • Hénonův atraktor
    • Kings Dream
• Dimenze
  • Topologická dimenze
  • Fraktální dimenze
    • Hausdorffova dimenze
    • Mřížková dimenze
• Fraktály
  • L-systémy (Lindenmayerovy systémy)
  • IFS (Iterated Function Systems)
  • TEA (polynomické fraktály)
    • Juliovy množiny
    • Mandelbrotova množina
  • Náhodné fraktály
  • Logistická funkce a bifurkační diagram
    • Logistická funkce
• Využití teorie chaosu v praxi
  • Biologie
    • Samoorganizace
    • Modelování populace
    • Kolonie bakterií
  • Fyzika
    • Dvojité kyvadlo
    • Turbulence
    • Kapající kohoutek
    • Komprese dat
  • Zdroje

---

Historie chaosu

Deterministické systémy - Newtonovské zákony

Slovo chaos pochází z řečtiny a v různých odvětvích má různý význam. V kosmologii starého Řecka byl chaos zároveň prapůvodní prázdnotou vesmíru a také podsvětím, kde přebývali mrtví. Počátkem křesťanství došlo k posunu významu ke slovu nepořádek. V metafyzice je opakem zákona a pořádku.

Počátky teorie chaosu vztahujeme již k Newtonovým teoriím. Uběhlo už něco málo přes tři sta let od publikace díla, které nemá v historii obdobu, Matematických principů přírodovědy Isaaca Newtona (obrázek). Stále se prodává okolo 700 výtisků ročně - nejčastěji studentům humanitních věd (studují z původních zdrojů). Poselství tohoto díla zní: V přírodě panují zákonitosti a my je můžeme najít.

Díky Newtonova zákona gravitace a pohybovému zákonu se vše zdálo předvídatelné. Jeho zákony se staly pro více než dvě století konečným popisem přírody. Najednou jsme mohli vysvětlit pohyb planet a měsíců, výskyt zatmění a komet. Vše velice přesně na několik století dopředu. Revoluce ve vědeckém myšlení, která vyvrcholila Newtonem, vedla k vizi světa jako obrovského mechanismu fungujícího jako “hodinový stroj” - k vyjádření naprosté spolehlivosti a mechanické dokonalosti. V takové vizi je stroj především předvídatelný. Za stejných podmínek provede stejné věci. Co vedlo vědce 17. a 18. století k takovému sterilnímu pohledu na náš svět? Newton zformuloval své zákony jako matematické rovnice, které dávají do poměru nejen veličiny, ale i míry změn těchto veličin. Když těleso padá volně pod vlivem konstantní gravitace, není to jeho poloha, co by zůstávalo neměnné. Není to ani jeho rychlost - míra změny polohy -, co by zůstávalo konstantní. Čím déle těleso padá, tím padá rychleji - je to zrychlení, neboli míra změny míry změny polohy - co se nemění. Rovnicím, ve kterých se vyskytují míry změn, se říká diferenciální rovnice. Míra změny veličiny je dána rozdílem jejich hodnot ve dvou blízkých okamžicích. Pro nás je důležité, že pokud známe počáteční polohy a rychlosti všech složek dynamického systému, tak je řešení rovnic popisujících pohyb tohoto systému jednoznačné. Pokud v nějakém daném okamžiku známe polohy a rychlosti všech částeček hmoty ve Sluneční soustavě, potom jsou všechny další pohyby těchto částic určené jednoznačně.

Toto předpokládá, že na pohyb nepůsobí žádné vnější vlivy. Pokud bychom se snažili vzít v potaz i tyto, vedlo by to k výkladu, že znalost poloh a rychlosti všech částic hmoty celého vesmíru v nějakém konkrétním okamžiku naprosto určuje jeho další vývoj. Vesmír sleduje jednoznačnou, předem danou dynamickou cestu.

Jeden z předních matematiků 18. století, Pierre Simon de Laplace ve svém Filozofickém pojednání o pravděpodobnostech píše:

“Kdyby existoval intelekt, který by v nějakém daném okamžiku znal všechny síly, které hýbou světem, vzájemné polohy všech bytostí, ze kterých se svět skládá, a byl by tak nesmírný, že by tato data znalyzoval, mohl by pohyby největších těles vesmíru i nejlehčího atomu soustředit do jediného vzorce: pro takový intelekt by nebylo nic nejisté a budoucnost, stejně jako minulost, by měl před očima.”

Zde se zrodil vzor klasického determinismu: když rovnice předepisují vývoj systému jednoznačně a neexistují žádné náhodné vnější vstupy, potom je jeho chování dáno jednoznačně jednou provždy.

Přejdeme už k příkladu chaosu, konkrétně k jednomu měsíci Saturnu, Hyperionu. Má nepravidelný tvar, je to vesmírná brambora. Jeho oběžná dráha je přesná a pravidelná, ale jeho chování na dráze je zvláštní. Hyperion dělá kotrmelce. Složité a nepravidelné. Nijak se přitom Newtonovým zákonům nevzpírá, jeho kotrmelce se řídí zákony gravitace a dynamiky.

Předpokládejme, že by kosmická sonda zaznamenala pohyby Hyperionu. Předpokládejme, že by na základě těchto záznamů byli vědci schopni co nejpřesněji předpovědět budoucí pohyb Hyperionu předurčený Newtonovými zákony. Poté své předpoklady porovnáme se skutečností a budeme předpokládat, že nevyjdou. A taky že nevyjdou. Chyba v předpovídání? Ne. Selhání Newtonových zákonů? Ne. Čeká se, že předpověď nevyjde kvůli Newtonovým zákonům. Náhodné vnější vlivy? (plynová mračna, magnetická pole, sluneční vítr)? Ne.

Je to neodmyslitelná vlastnost matematických rovnic v dynamice. Schopnost generovat pohyb natolik složitý, tak citlivý na měření, že vypadá jako náhodný. Tomuto se říká chaos.

Definice chaosu

Ve slovníku najdeme dvě definice slova chaos 1. zmatek, nepořádek 2. stav s vysokou neuspořádaností. Třetí, matematická definice je stochastické chování v deterministickém systému. S laplaceovským determinismem jsme se již setkali. Slovo stochastický znamená náhodný.

Deterministické chování je ovládané exaktními a neporušitelnými pravidly. Stochastické chování je pravý opak: bez zákonů a pravidel, řízené náhodou.

Takže chaos je nepravidelné chování podle přesných pravidel. Jako Hyperion.

Chaos je úplně stejně všední jako periodické cykly. Ale s periodickými cykly jsme se setkávali už několik staletí, kdežto na existenci chaosu jsme narazili teprve nedávno, takže na něj nejsme zvyklí.

V populárním tisku se přerodil v něco, čemu se říká “teorie chaosu”. Chaos je však pojem, který nemůže být odtržen od zbytku dynamiky. Také se můžete s teorií chaosu setkat pod názvy či obory jako jsou teorie nelineárních systémů, teorie dynamických systémů nebo nelineární dynamika. Slovo teorie může mít přinejmenším dva významy:

1. tvrzení o chování světa, záleží na tom, jak dostatečně dobře odpovídá přírodě
2. koherentní soubor matematických znalostí s jasnou konzistentní identitou, v tomto smyslu nejsou o správnosti žádné spory.

Nyní se objevila společnice teorie chaosu známá jako teorie komplexity. Teorie chaosu nám říká, že jednoduché systémy se mohou projevovat složitě, teorie komplexity říká, že složité systémy se mohou chovat “emergentně” jednoduše.

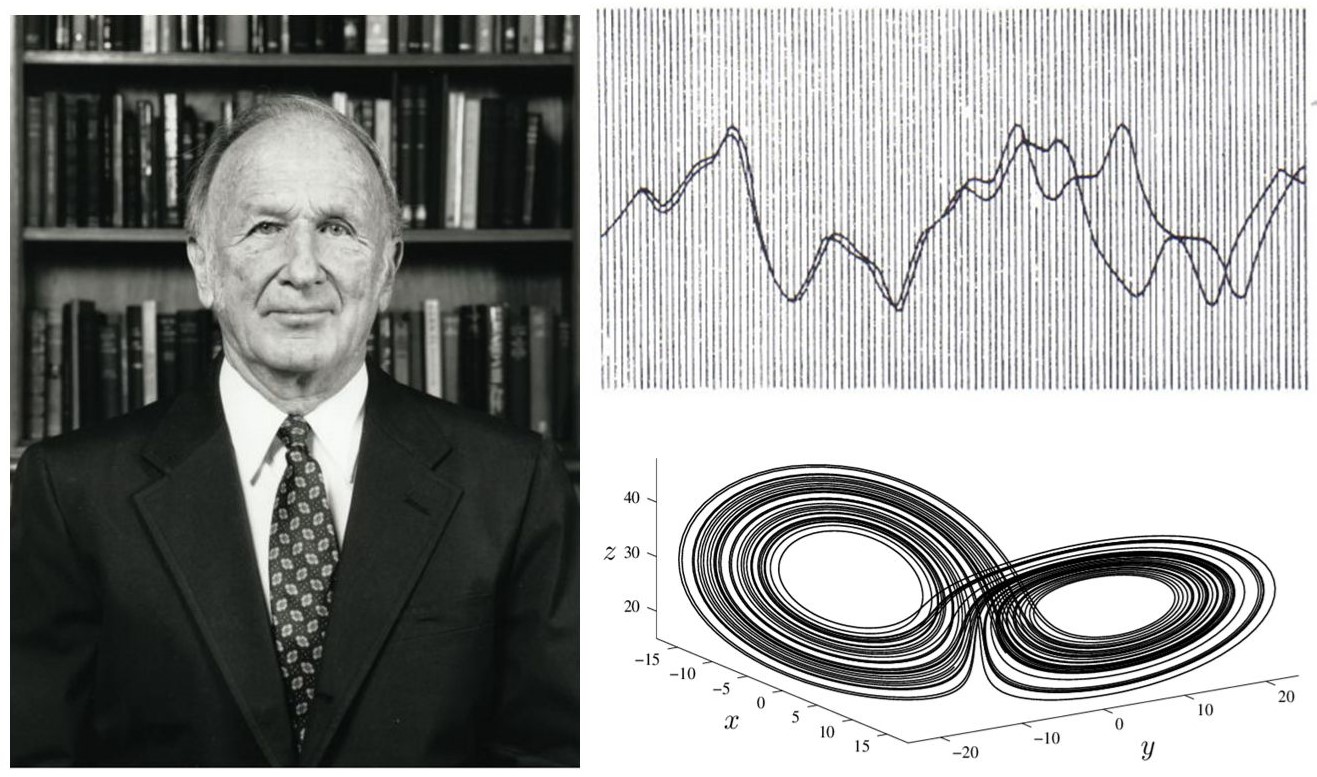
Velký zlom v teorii chaosu nastal s příchodem počítačů, které usnadnily výpočty, protože teorie chaosu je založená na opakovaném počítání stejných rovnic s různými hodnotami. Jednalo se především o výpočty Edwarda Lorenze, který se zabýval předpověďmi počasí. Jeho výpočty vedly k rozdílným výsledkům přestože zadáváná data se nepatrně lišila. Tento výsledek později nazval jako motýlí efekt.

Dynamické soustavy

Dynamickou soustavu (nebo systém) lze popsat pomocí stavového prostoru a dynamických podmínek. Souřadnice stavového prostoru popisují stav systému a dynamické podmínky změny stavů soustavy v čase.

Dynamické podmínky jsou obvykle zadány soustavou diferenciálních rovnic popisující změny stavového vektoru v čase.

Stavový prostor je množinou všech možných stavů, do kterých se může daný systém dostat. Existuje několik typů stavového prostoru. Těmi jsou stavové prostory konečné, nekonečné a spočitatelné. Konečný stavový prostor je takový prostor, který obsahuje konečný počet stavů (například balíček hracích karet). Spočitatelný stavový prostor obsahuje nekonečné množství stavů, ale každému stavu lze přiřadit jedno přirozené číslo. Nekonečný stavový prostor je prostor obsahující nekonečný počet stavů, jeho stavové proměnné jsou reálná čísla.

Dynamické soustavy lze rozdělit do několika typů:

• lineární
• nelineární
• deterministický
• stochastický

Lineární systém lze charakterizovat tak, že v něm lze uplatnit princip superpozice:

$$f(x) = a\\ f(y) = b$$

pak

$$f(x + y) = a + b$$

V lineárním systému lze předpovědět jeho vývoj a budoucnost.

V nelineárním systému neplatí princip superpozice a je nutné jej řešit pomocí diferenciálních rovnic a nelze zaručit jeho přesnou předpověď budoucího vývoje.

U deterministického systému lze předpovědět jeho budoucí vývoj a je jednoduché ho popsat.

U stochastického systému nelze předpovědět jeho budoucí vývoj. Je náhodný a je nutné se spolehnout pouze na statické funkce.

Chaotické chování

Systém vykazující chaotické chování musí splňovat následující podmínky:

Musí být citlivý na nastavení počátečních podmínek.

To znamená, že dvě blízké trajektorie ve fázovém prostoru se s rostoucím časem exponenciálně rozbíhají. Nebo-li malá změna v počátečních podmínkách může po čase vést k velmi odlišnému výsledku. Příkladem je tzv. motýlí efekt.

Musí být typologicky tranzitivní

Funkce:

$$f: X \rightarrow X,$$

je topologicky tranzitivní, jestliže pro každé dvě otevřené množiny:

$$A, B \subset X$$

existuje přirozené $n$ takové, že:

$$f^{n}(A) \cap B \neq \emptyset,$$

Jeho periodické orbity musí být husté

Orbita dynamického systému je část fázového prostoru systému, o které platí, že pokud se systém dostane do stavu, který náleží orbitě, potom všechny jeho další stavy do ní budou náležet také.

Tranzitivita, husté periodické body a citlivost na počáteční podmínky můžeme rozšířit na libovolný metrický prostor. J.Banks a jeho kolegové dokázali, že v nastavení obecného metrického prostoru tranzitivita a husté periodické podmínky implikují citlivost na počáteční podmínky.

Motýlí efekt

Termín motýlí efekt se vztahuje k citlivosti na počátečních podmínek chaotického systému. Jako první ho použil Edward Lorenz, při studiu atmosféry a pokusech o předpověď počasí. Při zadávání dat do počítače napsal hodnotu zaokrouhlenou na 0,506 místo 0,506127 a i přesto, že byla odchylka malá, vedla k velmi rozdílným výsledkům. Na základě těchto zjištění došel k závěru, že třeba pouhé mávnutí motýlích křídel může naprosto změnit počasí.

Atraktory

Vývoj dynamického systému se znázorňuje ve fázovém prostoru (diagramu). V takovém diagramu každá osa reprezentuje jednu dimenzi stavu. V průběhu vývoje systému lze ve fázovém prostoru pozorovat buď křivku, pokud je čas spojitý, nebo body, pokud je čas diskrétní. Mnohokrát je ve fázových diagramech vidět, že většina stavových trajektorií se přibližuje a omotává nějakou obecnou limitu. Atraktor dynamického systému je množina stavů, do kterých systém směřuje. Jinými slovy se jedná o množinu hodnot, kterých může nabývat stavový vektor dynamického systému po dostatečně dlouhém časovém úseku od počátečního impulsu, respektive od chvíle, kdy je systém inicializován.

Atraktorem je jakákoliv množina bodů, která má zjevnou tendenci směřovat k stabilnímu stavu nebo se v něm trvale pohybovat. Jedná se tedy o popis systému, který směřuje do jednoho určitého stabilního stavu.

Rozeznáváme několik typů atraktorů:

• pevné body
• periodické nebo kvaziperiodické
• chaotické
• podivné

Nejjednodušším případem atraktoru dynamických systémů jsou pevné body. Systém se v nekonečném čase ustálí v nějakém stabilním stavu, který je možné dopředu vypočítat. Příkladem může být kulička v prohlubni, která se ustálí v nejnižším bodě.

Pokud jsou atraktorem periodické nebo kvaziperiodické body, jedná se také o jednoduchý příklad. Dynamický systém osciluje mezi dvěma stavy. Může to být například obíhání vesmírné družice.

Jestliže atraktor systému je chaotický, pak nelze vývoj daného systému předem předpovědět. Tento systém vykazuje citlivost vůči počátečním podmínkám. Takovým systémem může být např. kulička na vrcholu kopce. Nikdy nevíme, kterým směrem se bude kutálet dolů.

Podivný atraktor je z hlediska teorie chaosu nejdůležitějším atraktorem. Chaotický pohyb vede k tomu, co je známé jako podivný traktor. Podivné atraktory vykazují velkou složitost a velkolepé detaily. Podivné atraktory se objevují jak ve spojitých dynamických systémech, jak je Lorenzův systém, tak i v některých diskrétních systémech, jako je Hénonovo zobrazení. Jiné diskrétní dynamické systémy mají odpuzující strukturu nazývanou Juliovy množiny, která tvoří hranici mezi oblastmi přitažlivosti pevných bodů. Juliovy množiny lze pokládat za podivné odpuzovače. Jak podivné atraktory, tak i Juliovy množiny mají typickou fraktální strukturu. Může vzniknout jen tehdy, je-li daný dynamický systém popsán nejméně třemi diferenciálními rovnicemi. Tento termín poprvé zavedl E. Lorenze a dosud není přesně matematicky definován. Obecně můžeme říci, že daný atraktor je podivný, pokud vykazuje stejné vlastnosti jako fraktály. Z tohoto tvrzení vyplývá, že každý podivný atraktor je fraktálem.

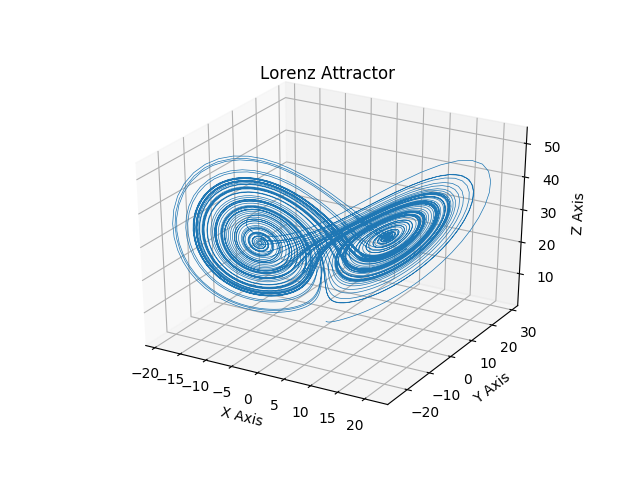
Lorenzův atraktor

Jedná se o trojrozměrnou strukturu, kterou roku 1963 představil Edward N. Lorenz. Popisuje nelineární deterministický dynamický systém odvozený z vynuceného proudění v atmosféře. Je popsána třemi diferenciálními rovnicemi. Tato struktura je spojitá a nikde se neprotíná.

$$\begin{align} \frac{dx}{dt} &= \delta (y -x),\notag \\ \frac{dy}{dt} &= x( \rho - z) - y,\notag\\ \frac{dz}{dt} &= xy - \beta z.\notag \end{align}$$

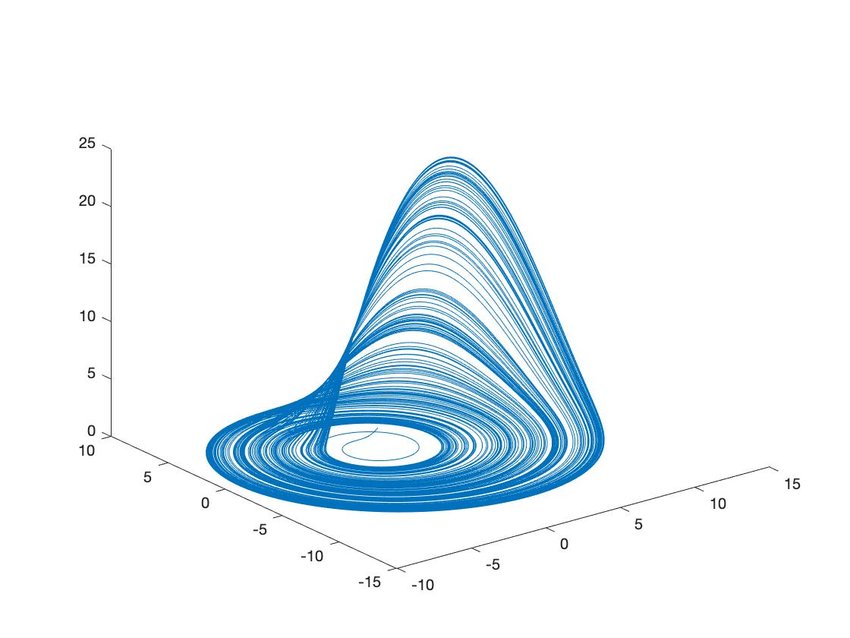
Rösslerův atraktor

Rösslerův atraktor je uměle vytvořený systém, který generuje chaos na základě jednoduchých transformací. Jedná se o transformace stretch a fold ( = rozprostření a ohyb). Byl vytvořen roku 1976 a jeho základem je o třináct let starší Lorenzův atraktor. Je popsán třemi diferenciálními rovnicemi.

$$\begin{align} \frac{dx}{dt} &= -y -z\notag\\ \frac{dy}{dt} &= x + ay\notag\\ \frac{dz}{dt} &= b + z (x-c)\notag \end{align}$$

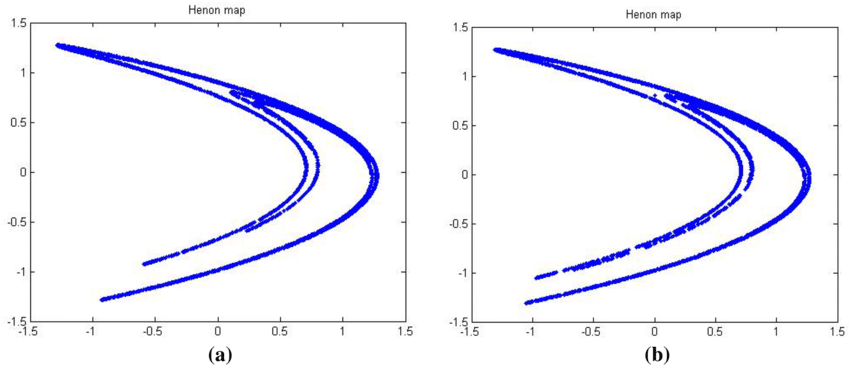
Hénonův atraktor

Hénonův atraktor je jeden z dvojdimenzionálních diskrétních atraktorů. Je založen na dvou rovnicích – jedné kvadratické, druhé lineární. Na začátku generování tohoto zobrazení jsou vykreslovány body, které spolu zdánlivě nesouvisejí.

Kings Dream

Atraktory neslouží pouze k osvětlení matematických nebo fyzikálních vlastností, ale mohou mít také estetickou funkci. Jedním z nich je Kings Dream, který byl vytvořen čistě za estetickým účelem.

Dimenze

Topologická dimenze

K tomu, abychom mohli definovat pojem fraktál, je nejprve nutné říct, co je to dimenze. Dimenze je počet vektorů báze daného prostoru, neboli počet souřadnic,které potřebujeme k jednoznačnému určení bodu v prostoru. Můžeme také říct, že je to počet rozměrů daného objektu.

Například dimenze roviny je 2, potřebujeme dvě souřadnice k určení bodu. Dimenze krychle je 3, má tři rozměry: šířka, výška, hloubka. Je-li hodnota dimenze celočíselná, pak řekneme, že toto číslo je topologickou dimenzí daného objektu. Topologická dimenze popisuje geometricky hladké objekty.

Fraktální dimenze

Fraktální dimenze říká, jak moc je daný útvar členitý. Existuje několik typů fraktálních dimenzí:

• Hausdorffova dimenze
• mřížková dimenze (box-counting dimension)
• informační dimenze
• korelační dimenze
• Ljapunovova dimenze
• Kolmogorovova entropie (Measure – Theoretic, Kolmogorov – Sinai, KS entropy)

Hausdorffova dimenze

Tato dimenze je definována pouze pro soběpodobné struktury. Pro soběpodobné útvary platí, že pokud je pozorujeme při jakémkoli měřítku, vidíme stále se opakující charakteristický tvar. Příklad: úsečka, čtverec.

Mřížková dimenze

Mřížkovou dimenzi lze – na rozdíl od Hausdorffovy dimenze – určovat pro libovolný útvar. Pro ustanovení této dimenze je nutné objekt vložit do mřížky a spočítat počet neprázdných čtverců mřížky.

Mylná představa je, že fraktály jsou perfektně soběpodobné útvary - např. Van Kochova vločka. Tyto útvary jsou úžasným příkladem, co fraktály jsou, ale sám Mandelbrot měl na mysli mnohem širší představu o fraktálech. A to ne jen aby představovaly krásné objekty, ale více pragmatickou představu a to tu, že popisují a ukazují objekty v přírodě a hlavně jejich členitost. Před Mandelbrotem existovalo pravidlo, že objekty jsou hladké, pokud zazoomujete dostatečně blízko - což Mandelbrotovi přišlo idealizované, protože takto zanedbávají detaily, na kterých záleží. Zpozoroval, že soběpodobné útvary dávají základ pro modelování pravidelnosti v některých formách členitosti. Opět ale představa, že fraktály jsou perfektně soběpodobné útvary, je příliš idealizovaná, protože jde proti jednomu ze základních principů fraktální geometrie. Opravdová definice fraktálu souvisí právě s fraktální dimenzí Pravdou je, že fraktální dimenze je vytvořený matematický koncept, ale ukazuje se, že to může být použitelný konstrukt k popisování světa a přírody.

Nejprve se podíváme na tři objekty, které ani nejsou fraktály a poté si to ukážeme na Sierpinského trojúhelníku - viz přednáška.

Fraktály

Za zakladatele fraktální geometrie je považován francouzský matematik Benoît Mandelbrot, který roku 1975 poprvé použil termín fraktál. Neexistuje žádná matematicky přesná definice pojmu fraktál. Nejblíže k tomu má asi původní Mandelbrotova definice: Fraktál je množina, jejíž Hausdorffova dimenze je větší než dimenze topologická. Tato definice říká, že fraktál je takový útvar, jehož dimenze je neceločíselná. Existují ovšem také výjimky, kdy za fraktály považujeme i útvary mající celočíselnou dimenzi. Fraktál lze také obecně definovat pomocí jeho vlastností: Fraktál je geometrický útvar, který lze rozdělit na části, přičemž tyto části jsou (alespoň přibližně) zmenšené kopie celého útvaru. Fraktál je soběpodobný a nezávislý na měřítku (invariace vůči měřítku). Další obecnou definicí založenou na vlastnostech fraktálů je: Fraktál je nekonečně členitý útvar.

Fraktály se rozdělují do několika typů:

• L-systémy
• IFS (Iterated Fuction Systems)
• TEA (polynomické fraktály)
• náhodné fraktály

L-systémy (Lindenmayerovy systémy)

L – systémy, také často nazývané fraktální křivky, byly poprvé použity v roce 1968 botanikem Aristidem Lindenmayerem k simulaci vývoje mnohobuněčných organismů. Jedná se o programovací jazyk, ve kterém je místo kurzoru želva (anglicky turtle), kterou uživatel ovládá pomocí základních příkazů. Těmito příkazy jsou pouze pohyb želvy vpřed, vzad, otáčení vlevo, vpravo a schování a vyjmutí ze zásobníku. Budeme je používat pro generování instrukcí pro kreslení, budeme pořád dokola přepisovat stringy a písmena rekurzivně Vždy obsahují abecedu, iniciátor a generátor (ukážu jak se definuje Cantorova množina pomocí stringů) Pomocí těchto fraktálů lze generovat útvary podobné rostlinám a jiným přírodním útvarům. Díky těmto vlastnostem jsou využívány v biologii, geologii a jiných přírodních vědách.

IFS (Iterated Function Systems)

Systém iterovaných funkcí je matematická metoda k vytváření fraktálů. Takto vytvořené fraktály jsou vždy soběpodobné. Ačkoli ze své podstaty mohou mít IFS fraktály libovolnou dimenzi, obvykle se modelují jako 2D objekty. IFS byly poprvé představeny Johnem Hutchinsonem v roce 1981. Nejpoužívanější metoda při generování fraktálů použitím IFS se jmenuje chaotic game (chaotická hra).

TEA (polynomické fraktály)

Jedná se o fraktály, které jsou popsané nějakou polynomickou funkcí; patří sem například Mandelbrotova množina a Juliovy množiny. Konstrukce těchto fraktálů je založena na mapování přitažlivosti pro různé oblasti nelineárního systému. Principem výpočtu je testování různých hodnot dosazováním do rovnice. Na tento výsledek opět aplikujeme stejné pravidlo. Polynomické fraktály jsou množiny komplexních čísel, pro které hodnoty funkce postupně konvergují ke konečné hodnotě. Přestože rovnice těchto fraktálů jsou často jednoduché, jejich výpočet je náročný, závislý na výpočetní síle a počtu iterací. Čím kvalitnější chceme výsledek, tím větší nároky klademe na výpočet. Výpočet nelze nijak urychlit, protože bez dosazení daného bodu do rovnice a provedení příslušného počtu iterací nelze rozhodnout, zda daný bod spadá do oblasti přitažlivosti.

Juliovy množiny

Jejich autory jsou Gaston Julia a Pierre Fatou, kteří popsali jejich konstrukci roku 1918. Základem je rovnice: rovnice kde $z$ a $c$ jsou komplexní čísla, přičemž $c$ je parametr charakterizující danou Juliovu množinu. Podle toho předpisu ověříme, jestli hodnota z nediverguje. Při praktickém výpočtu stačí, jestliže $z > 2$.

Mandelbrotova množina

První, kdo ji popsal, byl Pierre Fatou roku 1905. Díky složitosti výpočtů ji však nikdy neviděl. Až Mandelbrot, po němž je pojmenována, ji poprvé vykreslil. Mandelbrotova množina je jeden z nejznámějších fraktálů, respektive její okraj je fraktálem. Mandelbrotova množina je katalogem množin Juliových. Každému bodu Mandelbrotovy množiny odpovídá Juliova množina s parametrem daným souřadnicemi tohoto bodu. Je definována jako množina komplexních čísel $\C$, pro které platí rekurzivní vzorec:

$$\begin{align} Z_1 &= 0 \notag\\ Z_{n+1} &= z_{n}^2 + c\notag \end{align}$$

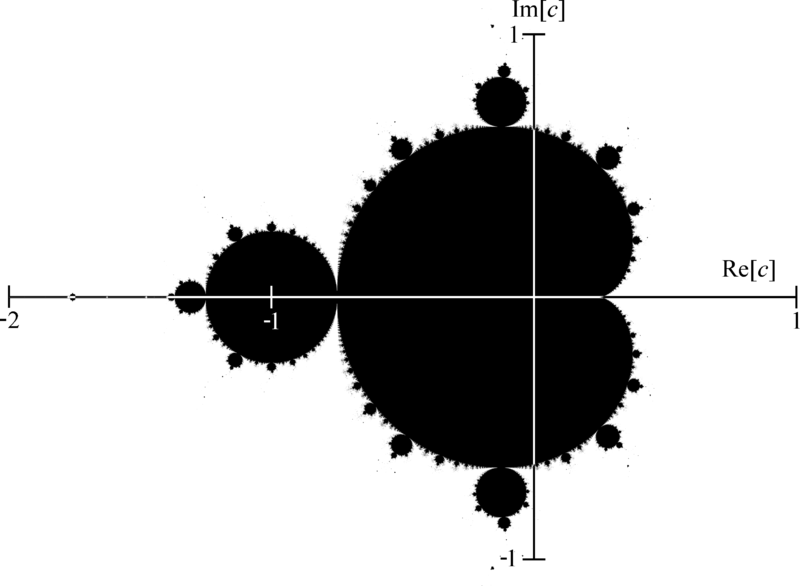
Náhodné fraktály

Většina fraktálů je určitým způsobem symetrická a obrazce, jež tímto způsobem vzniknou, neodpovídají příliš reálným objektům, i když se jim často podobají. To je dáno tím, že se v živé přírodě nevyskytuje příliš souměrnost. Abychom dostali obrazy lépe odpovídající skutečnosti, je nutné obohatit generování fraktálů o určitý prvek náhody. Tato nahodilost bude mít vliv na tvar výsledného fraktálu i jeho Hausdorffovu dimenzi. Existuje několik způsobů, jak lze generovat náhodné fraktály:

Pro generování náhody lze využít gaussovský generátor, či generátor bílého šumu.

Logistická funkce a bifurkační diagram

Logistická funkce

Logistická funkce je dalším případem chaotického chování. Tato funkce popisuje růst nějaké množiny a při určitých parametrech může dojít k chaotickému chování. Logistická rovnice se uplatňuje v mnoha oblastech vědy jako je biologie (modelování růstu populace), ekonomie, fyzika, chemie, medicína (růst nádorů), statistika a pravděpodobnost, umělé neuronové sítě a další. Podle oboru, kde se používá, se může lišit její vyjádření. Chaotické chování lze nejlépe ukázat na biologické aplikaci této funkce. Užívá se zde ve tvaru:

$$x_{n+1} = rx_n(1-x_n)$$

Jev, kdy v systému při malé změně řídícího parametru dojde k náhlé a výrazné změně vnitřního stavu systému, nazýváme bifurkací. Pro studium tohoto jevu slouží bifurkační diagram, do kterého se na osu $x$ vynáší hodnota řídícího parametru a na osu $y$ hodnota vnitřního stavu.

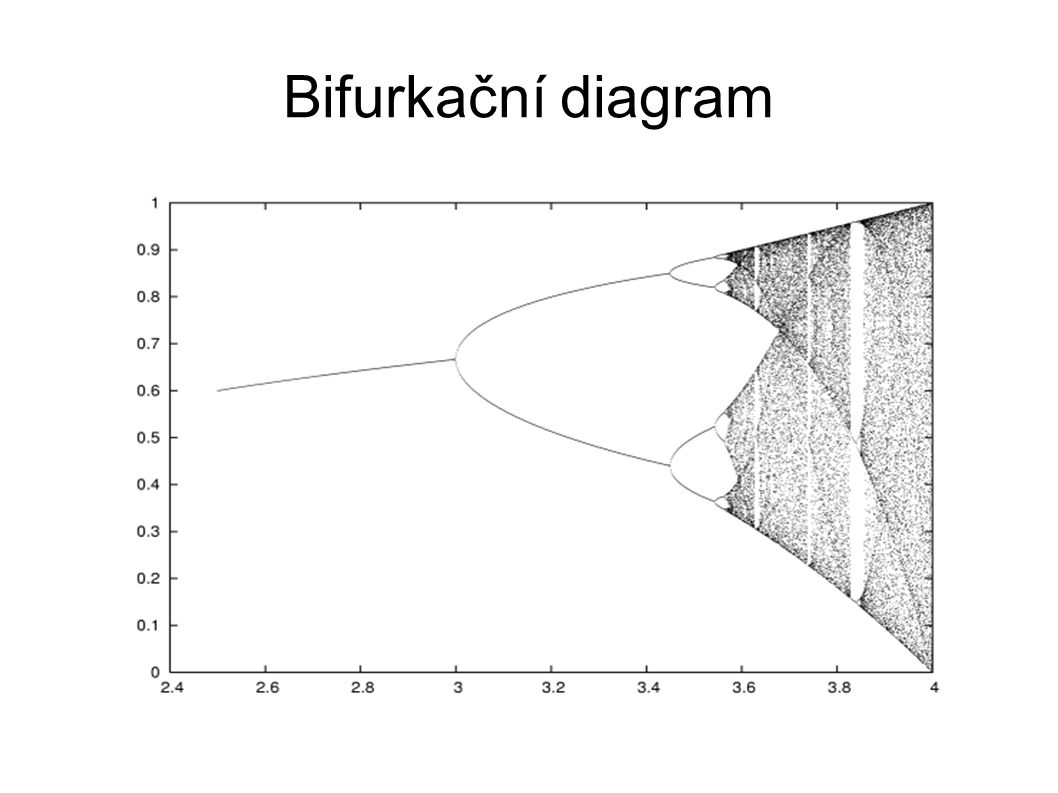
Využití teorie chaosu v praxi

Biologie

Samoorganizace

Samoorganizaci lze definovat jako jev, kdy se samostatné jednotky začnou chovat jako celek. Samoorganizační schopnost souvisí s tou částí teorie chaosu, která zahrnuje kvantovou mechaniku. Tento celek pak může vykazovat chaotické chování, nebo vytvářet fraktální struktury.

Příklady:

• kolektivní chování - hejna ptáků a ryb
• balení proteinů a jiných biomakromolekul (folding)

Modelování populace

Viz logistická funkce přednáška

Kolonie bakterií

Kolonie bakterií jsou při bližším pozorování ukázkou přírodních fraktálů a samoorganizace.

Fyzika

Dvojité kyvadlo

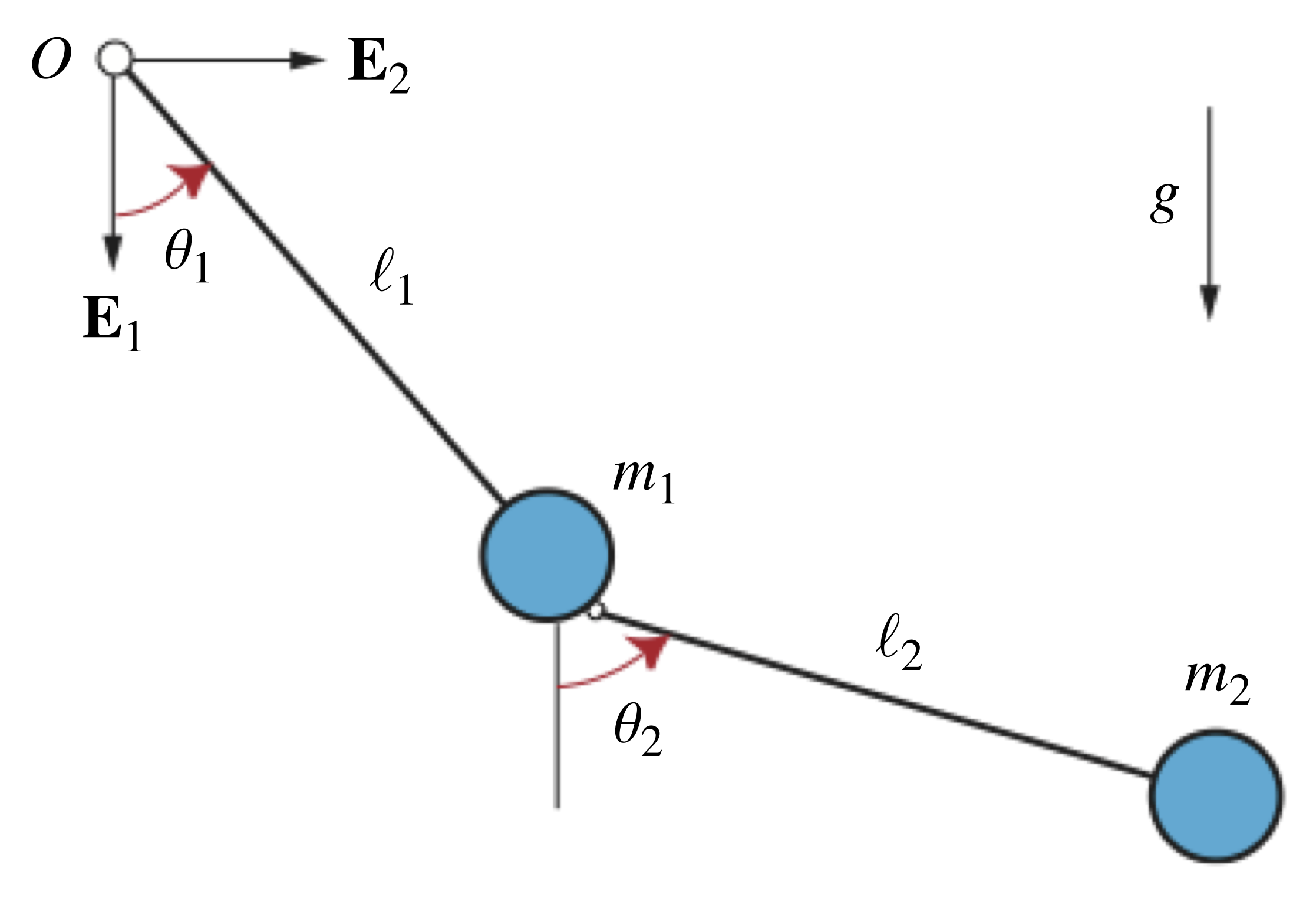
Dvojité kyvadlo je typickým příkladem chaotického systému. Složíme ho ze dvou jednoduchých kyvadel tak, že jejich konce volně spojíme, aby se mohla pohybovat. Pohyb dvojitého kyvadla je nutné popisovat diferenciálními rovnicemi a je velice citlivý na počáteční podmínky.

Turbulence

Turbulence, svatý grál fyziky, se také někdy označuje jako problém s rodokmenem, protože tento jev zkoumali všichni slavní fyzikové. Slavný fyzik Werner Heisenberg, který studoval kvantovou teorii, prý na smrtelném loži řekl, že bude mít na Boha dvě otázky. Proč relativita a proč turbulence. A na to prohlásil:

„Opravdu věřím, že na první otázku by mohl mít odpověď.“

Kapající kohoutek

Komprese dat

Komprese obrazu je založena na znalostech IFS fraktálů. Princip komprese spočívá v rozdělení obrazu na dva typy bloků. Prvním typem jsou range bloky, které se nepřekrývají, a druhým typem jsou domain bloky, které se mohou překrývat a jsou podobné range blokům.

---

Zdroje

Při vytváření tohoto článku jsem použila tyto zdroje:

James Gleick Chaos - vznik nové vědy
Ian Stweard Hraje Bůh kostky?
Diplomová práce Nelineární fyzika a teorie chaosu
Diplomová práce Synchronizace a komunikace pomocí deterministického chaosu v prostředí Mathematica
Video od 3Blue1Brown Fractals are typically not self-similar
Video od Veritasium Chaos: The Science of the Butterfly effect
Video od Veritasium This equation will change how you see the world

---